Adding Ambient Occlusion To Our Voxel Mesher

Ambient Occlusion is a visual effect that adds depth to your voxel game by making intersections between voxels darker, mimicking the way light interacts with corners in the real world.

In contrast to the absolutely stunning featured image, this is what our world looked like in part one:

Ew! What even are those dark squares?

The sides of the voxels, of course! … and now you see why Ambient Occlusion is so necessary.

Without the depth queues that the gentle shadowing gives us, there is no way for us to visually distinguish the different heights of the terrain.

So let’s implement it.

Defining the Problem

With Ambient Occlusion enabled, each Face that our mesher outputs will have four additional occlusion values (one per vertex), representing how much each vertex should be shaded via occlusion.

We will calculate AO values after generating the mesh, as the AO algorithm operates on faces instead of voxels.

First, since calculating Ambient Occlusion may be expensive, we add a separate iter_with_ao method to QuadGroups:

impl QuadGroups {
    // ...

    pub fn iter_with_ao<'a, C, V>(&'a self, chunk: &'a C) -> impl Iterator<Item = FaceWithAO<'a>>
    where
        C: Chunk<Output = V>,
        V: Voxel,
    {
        self.iter().map(|face| FaceWithAO::new(face, chunk))
    }
}

Next, we create the FaceWithAO type:

impl QuadGroups {
    // ...

    pub fn iter_with_ao<'a, C, V>(&'a self, chunk: &'a C) -> impl Iterator<Item = FaceWithAO<'a>>
    where
        C: Chunk<Output = V>,
        V: Voxel,
    {
        self.iter().map(|face| FaceWithAO::new(face, chunk))
    }
}

// ...

pub(crate) fn face_aos<C, V>(face: &Face, chunk: &C) -> [u32; 4]
where
    C: Chunk<Output = V>,
    V: Voxel,
{
    todo!()
}

pub struct FaceWithAO<'a> {
    face: Face<'a>,
    aos: [u32; 4],
}

impl<'a> FaceWithAO<'a> {
    pub fn new<C, V>(face: Face<'a>, chunk: &C) -> Self
    where
        C: Chunk<Output = V>,
        V: Voxel,
    {
        let aos = face_aos(&face, chunk);
        Self { face, aos }
    }

    pub fn aos(&self) -> [u32; 4] {
        self.aos
    }
}

Why are we passing the chunk into the iterator?

Even though it doesn’t iterate over the voxels, FaceWithAO still needs the voxels to calculate the AO values. This is almost like we are performing another meshing pass.

… then why not just do it in the mesher itself?

Because this is easier to implement. We won’t need to change the mesher itself to support AO.

Moving on, you’ll notice that we left face_aos unimplemented:

pub(crate) fn face_aos<C, V>(face: &Face, chunk: &C) -> [u32; 4]
where
    C: Chunk<Output = V>,
    V: Voxel,
{
    todo!()
}

This method takes in the underlying Face and a reference to our Chunk, and returns four u32 occlusion values.

We’ll need to know what those values mean in order to implement it.

Occlusion Values

For each vertex, there are four different possible occlusion values.

In this image, 0 is represented by the red channel, 1 by the green channel, 2 by the blue channel, and 3 by pure white. The shader smoothly blends the values over each face, producing a gradient.

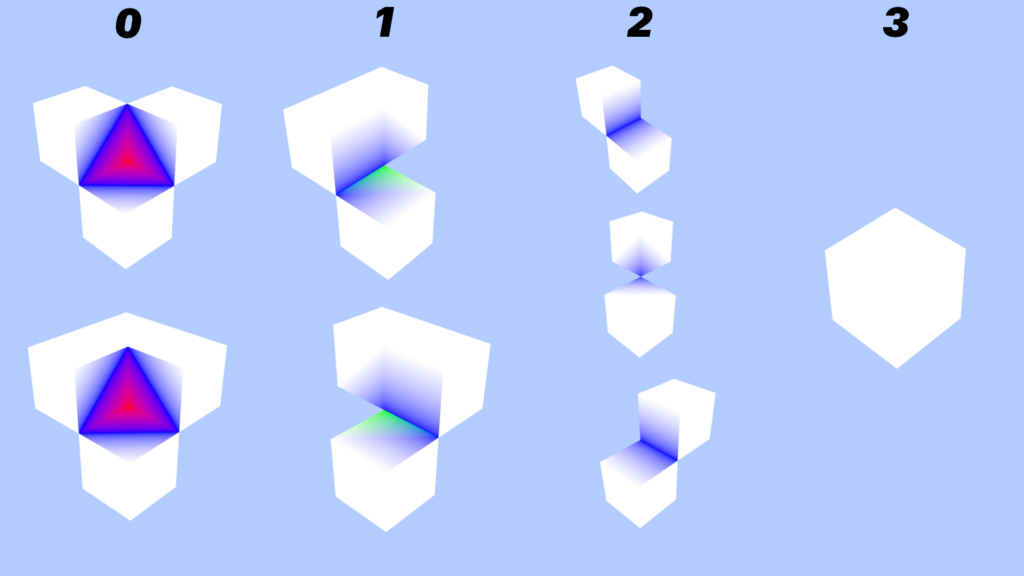
With this, we can see the rule is:

• 0 if both voxels on the sides of the vertex are opaque
• 1 if exactly one of the voxels on the side and the voxel in the corner are opaque
• 2 if exactly one of adjacent voxels is opaque
• 3 if none of the adjacent voxels are opaque

… and in code:

// true if OPAQUE, otherwise false
pub(crate) fn ao_value(side1: bool, corner: bool, side2: bool) -> u32 {
    match (side1, corner, side2) {
        (true, _, true) => 0,
        (true, true, false) | (false, true, true) => 1,
        (false, false, false) => 3,
        _ => 2,
    }
}

If there are only four possible values, why are we using a u32?

Due to a limitation of our engine, u32 is the smallest value we can send to the shader. We use u32 here to avoid having to convert it later.

If you don’t care about conversion (or if your engine doesn’t have this limitation), a u8 or an enum would be perfectly acceptable here.

Test

Now that we’ve made some good progress, let’s test it out.

This is what our mesh builder currently looks like:

fn main() {
    // ...

    let result = simple_mesh(&chunk);

    let mut positions = Vec::new();
    let mut indices = Vec::new();
    let mut normals = Vec::new();
    let mut uvs = Vec::new();

    for face in result.iter() {
        positions.extend_from_slice(&face.positions(1.0));
        indices.extend_from_slice(&face.indices(positions.len() as u32));
        normals.extend_from_slice(&face.normals());
        uvs.extend_from_slice(&face.uvs(false, true));
    }

    // engine-specific mesh creation
    
    // ...
}

After returning from the mesher we iterate over each face in QuadGroups, building a Vec from each value.

We’ll update this method to use iter_with_ao and build a Vec of occlusion values:

fn main() {
    // ...

    let result = simple_mesh(&chunk);

    let mut positions = Vec::new();
    let mut indices = Vec::new();
    let mut normals = Vec::new();
    let mut uvs = Vec::new();
    let mut aos = Vec::new();

    for face in result.iter_with_ao(&chunk) {
        positions.extend_from_slice(&face.positions(1.0));
        indices.extend_from_slice(&face.indices(positions.len() as u32));
        normals.extend_from_slice(&face.normals());
        uvs.extend_from_slice(&face.uvs(false, true));
        aos.extend_from_slice(&face.aos());
    }

    // engine-specific mesh creation
    
    // ...
}

Let’s see the output.

error[E0599]: no method named `positions` found for struct `FaceWithAO` in the current scope
error[E0599]: no method named `indices` found for struct `FaceWithAO` in the current scope
error[E0599]: no method named `normals` found for struct `FaceWithAO` in the current scope
error[E0599]: no method named `uvs` found for struct `FaceWithAO` in the current scope

Right.

We have six options here:

1. Make the face field of FaceWithAO public
2. Add a getter method to FaceWithAO which returns a reference to its Face
3. Implement all of the Face methods manually on FaceWithAO
4. Create a impl_face macro
5. Turn Face into a trait
6. Implement Deref<Target=Face for FaceWithAO

Options 1 and 2 are unergonomic. When calling methods on Face you’ll need to vary your access pattern via whether you are getting the AO value or not.

Options 3 and 4 are stupid.

Option 5 is a good idea, but requires way too much boilerplate for only two types.

Option 6 is perfect. Auto-deref means that whenever we call a method on FaceWithAO it will fall back to Face if it can’t be found on FaceWithAO.

impl<'a> Deref for FaceWithAO<'a> {
    type Target = Face<'a>;

    fn deref(&self) -> &Self::Target {
        &self.face
    }
}

Hmm… Are you sure this is a good idea? Reading the docs, I see this:
Deref should only be implemented for smart pointers to avoid confusion.

It would probably be a bad idea if FaceWithAO was generally used outside of an iterator. Since we don’t need to do anything with FaceWithAO except extract values from it, we don’t need to care.

Let’s try it again.

thread 'main' panicked at 'not yet implemented'

Great, let’s move on.

Indices

For each vertex in the Face, we will calculate the occlusion value with its three neighbors via the ao_value method we defined earlier. We will then have to return the values in a standardized order.

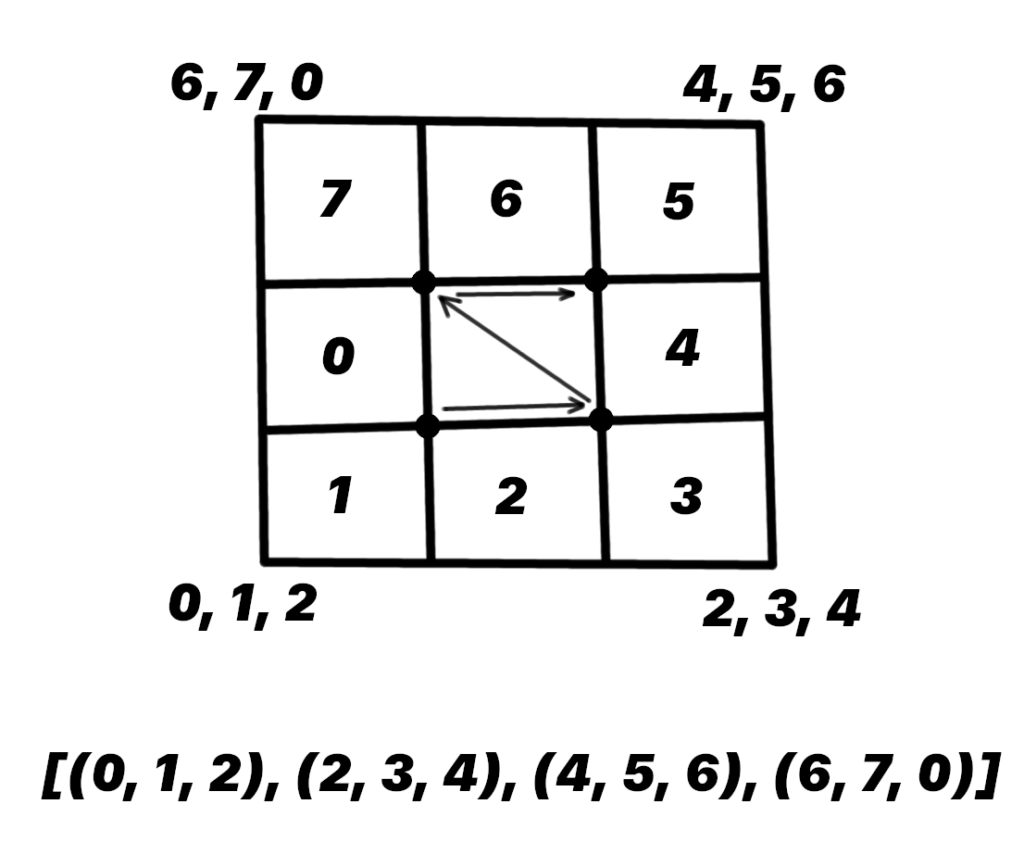
Recall that we output our positions in the order bottom-left, bottom-right, top-left, top-right. We’ll use the same order here.

We define side_aos as a method that accepts an array of the face’s eight neighbors, which returns the four occlusion values for the Quad:

pub(crate) fn side_aos<V: Voxel>(neighbors: [V; 8]) -> [u32; 4] {
    let ns = [
        neighbors[0].visibility() == OPAQUE,
        neighbors[1].visibility() == OPAQUE,
        neighbors[2].visibility() == OPAQUE,
        neighbors[3].visibility() == OPAQUE,
        neighbors[4].visibility() == OPAQUE,
        neighbors[5].visibility() == OPAQUE,
        neighbors[6].visibility() == OPAQUE,
        neighbors[7].visibility() == OPAQUE,
    ];

    [
        ao_value(ns[0], ns[1], ns[2]),
        ao_value(ns[2], ns[3], ns[4]),
        ao_value(ns[6], ns[7], ns[0]),
        ao_value(ns[4], ns[5], ns[6]),
    ]
}

Great, but I still can’t call this method. What neighbors does it need, exactly?

Each face will need the neighbors of the face itself. For example, if we take the face with voxel (1,1,1), and a X-Negative side, it would need the neighbors [(0,1,2), (0,0,2), (0,0,1), (0,0,0), (0,1,0), (0,2,0), (0,2,1), (0,2,2)].

That’s a lot to remember.

Yes, but as always there’s a rule we can use to generate them. We’ll take a look at that in the next section.

Offsets

We’ll use the Right-Hand Y-Up coordinate system to determine which offsets we will need for each face’s neighbors.

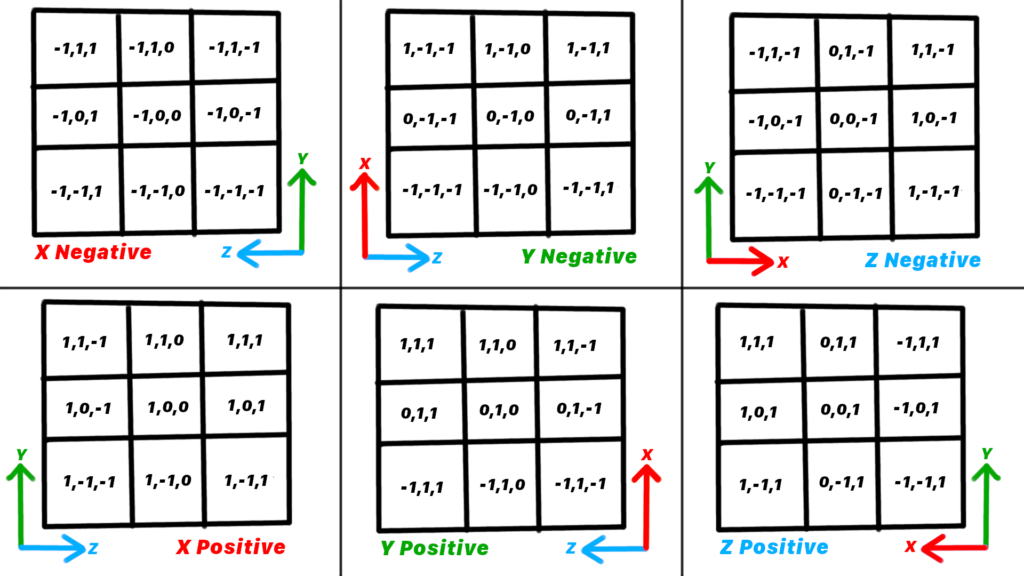
With the order we specified above, we’ll return the value in the middle on the left hand side then continue counter-clockwise. We will ignore the center value.

We will use these offsets to get each neighboring voxel and pass it into our side_aos method.

pub(crate) fn face_aos<C, V>(face: &Face, chunk: &C) -> [u32; 4]
where
    C: Chunk<Output = V>,
    V: Voxel,
{
    let [x, y, z] = face.voxel();

    match face.side() {
        Side::X_NEG => side_aos([
            chunk.get(x - 1, y, z + 1),
            chunk.get(x - 1, y - 1, z + 1),
            chunk.get(x - 1, y - 1, z),
            chunk.get(x - 1, y - 1, z - 1),
            chunk.get(x - 1, y, z - 1),
            chunk.get(x - 1, y + 1, z - 1),
            chunk.get(x - 1, y + 1, z),
            chunk.get(x - 1, y + 1, z + 1),
        ]),
        Side::X_POS => side_aos([
            chunk.get(x + 1, y, z - 1),
            chunk.get(x + 1, y - 1, z - 1),
            chunk.get(x + 1, y - 1, z),
            chunk.get(x + 1, y - 1, z + 1),
            chunk.get(x + 1, y, z + 1),
            chunk.get(x + 1, y + 1, z + 1),
            chunk.get(x + 1, y + 1, z),
            chunk.get(x + 1, y + 1, z - 1),
        ]),
        Side::Y_NEG => side_aos([
            chunk.get(x - 1, y - 1, z),
            chunk.get(x - 1, y - 1, z + 1),
            chunk.get(x, y - 1, z + 1),
            chunk.get(x + 1, y - 1, z + 1),
            chunk.get(x + 1, y - 1, z),
            chunk.get(x + 1, y - 1, z - 1),
            chunk.get(x, y - 1, z - 1),
            chunk.get(x - 1, y - 1, z - 1),
        ]),
        Side::Y_POS => side_aos([
            chunk.get(x, y + 1, z + 1),
            chunk.get(x - 1, y + 1, z + 1),
            chunk.get(x - 1, y + 1, z),
            chunk.get(x - 1, y + 1, z - 1),
            chunk.get(x, y + 1, z - 1),
            chunk.get(x + 1, y + 1, z - 1),
            chunk.get(x + 1, y + 1, z),
            chunk.get(x + 1, y + 1, z + 1),
        ]),
        Side::Z_NEG => side_aos([
            chunk.get(x - 1, y, z - 1),
            chunk.get(x - 1, y - 1, z - 1),
            chunk.get(x, y - 1, z - 1),
            chunk.get(x + 1, y - 1, z - 1),
            chunk.get(x + 1, y, z - 1),
            chunk.get(x + 1, y + 1, z - 1),
            chunk.get(x, y + 1, z - 1),
            chunk.get(x - 1, y + 1, z - 1),
        ]),
        Side::Z_POS => side_aos([
            chunk.get(x + 1, y, z + 1),
            chunk.get(x + 1, y - 1, z + 1),
            chunk.get(x, y - 1, z + 1),
            chunk.get(x - 1, y - 1, z + 1),
            chunk.get(x - 1, y, z + 1),
            chunk.get(x - 1, y + 1, z + 1),
            chunk.get(x, y + 1, z + 1),
            chunk.get(x + 1, y + 1, z + 1),
        ]),
    }
}

That’s a huge match statement! Is there a simpler way to do this?

Maybe, but if there is I haven’t found it yet.

I’ll leave that as an exercise for the reader.

So that’s it, then?

Almost! We’ll need to actually convert these occlusion values into occlusion colors before they can be rendered, though.

Occlusion Colors

Exactly how you apply occlusion colors to your mesh is project specific. Usually, you will either pass the occlusion value into the shader and calculate the color on the GPU, or calculate the occlusion color on the CPU and pass it in as the vertex color.

Either way, you’ll eventually end up matching the occlusion value and outputting a color:

fn ao_color(ao: u32) -> vec4<f32> {
    switch ao {
        case 0u {
            return vec4<f32>(0.1, 0.1, 0.1, 1.0);
        }
        case 1u {
            return vec4<f32>(0.25, 0.25, 0.25, 1.0);
        }
        case 2u {
            return vec4<f32>(0.5, 0.5, 0.5, 1.0);
        }
        default {
            return vec4<f32>(1.0, 1.0, 1.0, 1.0);
        }
    }
}

The real question is what color?

In our case, we directly multiply the occlusion color with the sampled texture color and pass it into PBR:

@fragment
fn fragment(in: FragmentInput) -> @location(0) vec4<f32> {
  var pbr_input: PbrInput = pbr_input_new();
  
  // ...

  pbr_input.material.base_color = color * in.ao_color;

  // ...
}

It might not be the most physically accurate way to do it, but this is really just an artistic choice.

As for what colors you should use, it’s up to you! Just pick whatever looks good.

Awesome.

With all that out of the way, let’s see what it looks like.

Yay! … but it doesn’t look quite right.

We’ve ran into the next problem, anisotropy.

Anisotropy

Splitting quads into triangles introduces a problem known as anisotropy. Depending on the orientation, occlusion may be displayed incorrectly.

To fix this, we will introduce a consistent orientation for our quads. We’ll swap the indices around if the occlusion values would introduce anisotropy.

impl<'a> FaceWithAO<'a> {
    // ...
    
    pub fn indices(&self, start: u32) -> [u32; 6] {
        let aos = self.aos();

        if (aos[1] + aos[2]) > (aos[0] + aos[3]) {
            [start, start + 2, start + 1, start + 1, start + 2, start + 3]
        } else {
            [start, start + 3, start + 1, start, start + 2, start + 3]
        }
    }
}

Now I see why we used Deref …

Yep. Now let’s see what this looks like:

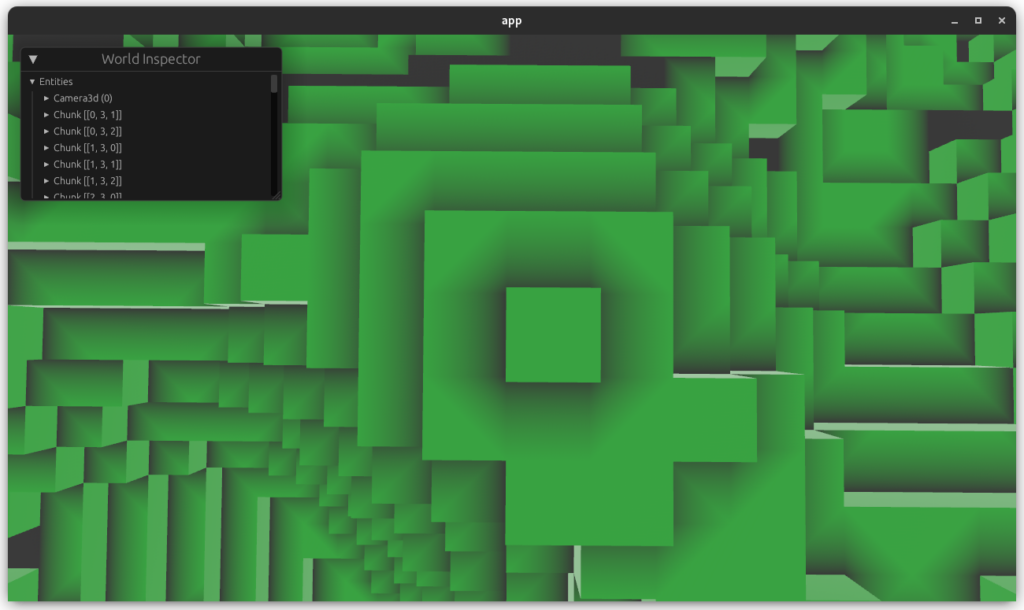
Hooray!

Results

Side by side, before and after implementing ambient occlusion.

It’s not even close.

Next Steps

Our implementation of ambient occlusion is acceptable, but imperfect. Here is what we missed.

Chunk Boundary

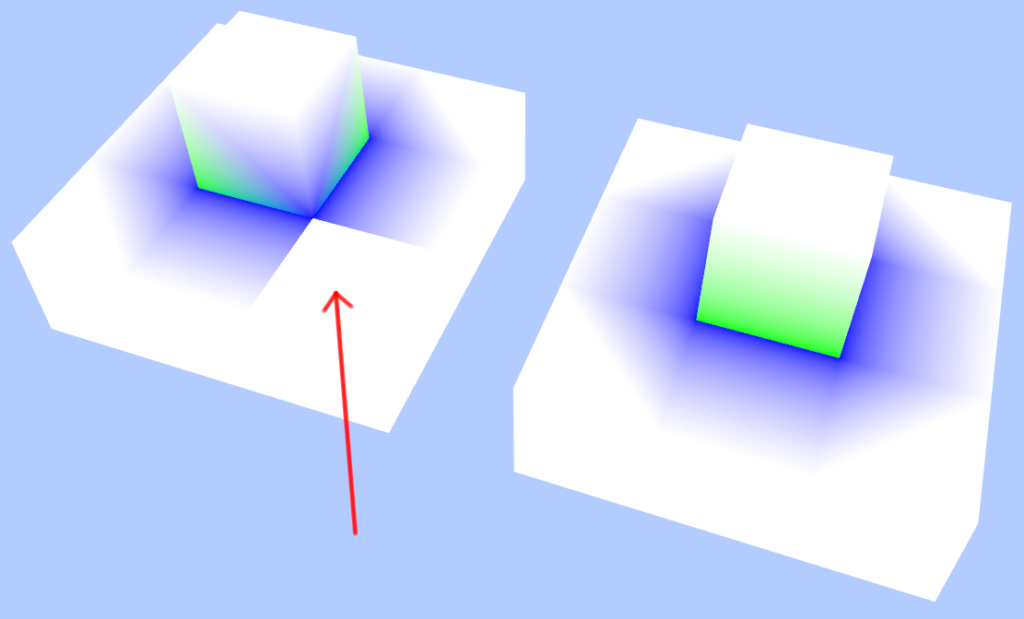
In part one of this series, we said that you would only need to include the six direct neighbors in the chunk boundary. While that might have been true before, it isn’t anymore.

You’ll need to include all 26 neighbors to get accurate occlusion.

Greedy Meshing

Very nearly all of the code we’ve written today has assumed you are using unit-sized quads. Of course this won’t be the case if you’re doing Greedy Meshing.

If you are, though – you should consider not doing it.

We might follow up on this in a later entry of this series.

Source

Ripped verbatim from the game, might need some tweaks to compile by itself.